新NISAでオルカンに全財産を一括投資した結果 25/02/28(+122)

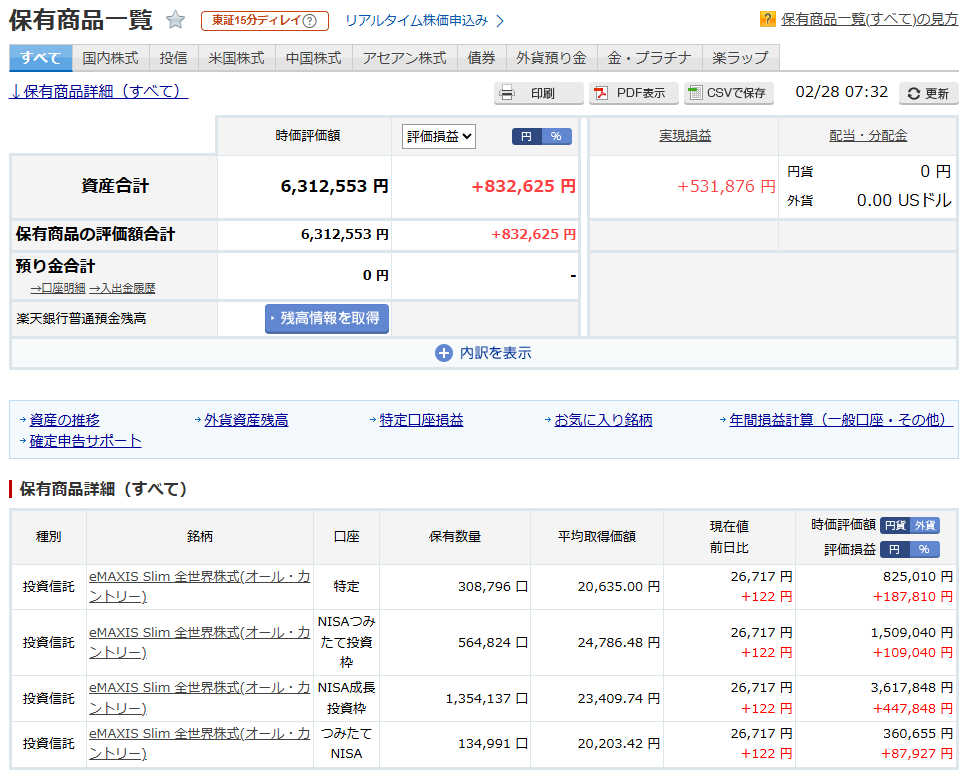
現在の運用実績です。

圏論とは何か

はい、圏論の概要について解説します。専門家として、客観的かつ中立的な立場から、シンプルな日本語で説明します。

圏論とは何か？：抽象化による数学の構造化

圏論は、数学的な構造とその間の関係性を抽象的に扱うための枠組みです。圏論を用いることで、個々の数学的対象（例えば、集合、群、位相空間など）の詳細に立ち入ることなく、それらに共通する構造や性質を議論することができます。

なぜ圏論が必要なのか？：異なる分野の架け橋

圏論の主な利点は、異なる数学の分野（例えば、代数学、トポロジー、論理学など）を横断して適用できる点にあります。これにより、一見すると全く異なる分野の間に、驚くべき類似性や関係性を見出すことが可能になります。圏論は、数学全体の「共通言語」または「骨格」のような役割を果たします。

圏論の基本的な構成要素：対象、射、合成

圏論は、主に次の3つの要素から構成されます。

1. 対象 (Object)：
   • 圏論における「対象」は、集合、群、位相空間といった具体的な数学的対象だけでなく、より抽象的な概念も含むことができます。
   • 重要なのは、対象そのものの詳細ではなく、対象間の関係性です。
2. 射 (Morphism)：
   • 「射」は、対象間の関係性を表します。
   • 例えば、集合間の写像、群の準同型、位相空間の間の連続写像などが射の例です。
   • 射は、f: A → B のように表され、対象 A から対象 B への関係を示します。
3. 合成 (Composition)：
   • 「合成」は、2つの射を組み合わせて新しい射を作る操作です。
   • 射 f: A → B と射 g: B → C があるとき、これらの合成は g ∘ f: A → C と表され、対象 A から対象 C への射となります。
   • 合成は、結合法則を満たす必要があります（つまり、h ∘ (g ∘ f) = (h ∘ g) ∘ f が成り立つ）。

圏論における重要な概念：関手、自然変換

圏論では、圏と圏の関係性を記述するために、以下の概念が用いられます。

1. 関手 (Functor)：
   • 「関手」は、圏と圏の間の「構造を保つ写像」です。
   • 関手は、一方の圏の対象を他方の圏の対象に、射を射に対応させます。
   • この対応は、射の合成を保つ必要があります。
2. 自然変換 (Natural Transformation)：
   • 「自然変換」は、2つの関手の間の関係性を表します。
   • 自然変換は、一方の関手によって得られる対象を、他方の関手によって得られる対象へと「自然に」結びつけます。

圏論の応用例：多様な分野での活躍

圏論は、純粋数学の様々な分野（代数トポロジー、代数幾何学、表現論など）で用いられるだけでなく、理論計算機科学（プログラミング言語の意味論、型理論など）や、近年では量子情報理論、さらには認知科学など、幅広い分野で応用されています。

まとめ：圏論は数学の構造を捉える強力な道具

圏論は、数学的な構造を抽象化し、異なる分野間の関係性を明らかにするための強力な道具です。圏論の基本的な概念（対象、射、合成、関手、自然変換）を理解することで、数学全体の理解を深めることができるでしょう。

はい、その理解で概ね正しいです。圏論の核心を非常にシンプルに捉えています。

もう少しだけ正確に表現すると、以下のようになります。

• 「極限まで抽象化」: これは圏論の重要な側面です。個々の数学的対象（集合、群、ベクトル空間など）の具体的な性質を取り払い、それらの間の「関係性」（射）に焦点を当てます。
• 「共通の要素で表せるようにした」: これも圏論の目的の一つです。異なる分野に現れる構造を、圏、対象、射、関手、自然変換といった共通の概念で記述することで、分野間の類似性や関連性を明確にします。

圏論は、単に「共通の要素で表す」だけでなく、その「共通の構造」を使って、異なる分野間で定理や概念を翻訳したり、新しい視点を提供したりすることを可能にします。これが圏論の強力さの源泉です。

その質問は非常に興味深く、圏論の可能性と限界に関わる重要な点です。

理論的には可能だが、現実的には限界がある というのが答えになります。以下に詳細を説明します。

理論的な可能性

圏論は非常に強力な抽象化の道具であり、原理的には、ほとんどすべての数学的構造を圏、対象、射、関手、自然変換などの概念を用いて表現できます。多くの数学の分野が圏論の言葉で再定式化されており、それによって新たな洞察が得られたり、異なる分野間の関連性が見出されたりしています。

現実的な限界

しかし、「あらゆる数学分野の定理や概念が、圏論で 有用な形で 表せるか」というと、必ずしもそうではありません。限界としては、主に以下の点が挙げられます。

1. 抽象化の度合い:
   • 圏論は非常に抽象的なため、具体的な計算や個別の対象の詳細な性質を扱うには不向きな場合があります。例えば、特定の微分方程式の解を具体的に求めたい場合、圏論的な記述は直接的な助けにはならないでしょう。
   • 圏論は「構造」に焦点を当てるため、構造を持たない、あるいは構造が重要でない問題を扱うのは得意ではありません。
2. 表現の複雑さ:
   • ある分野の概念を圏論で表現することが可能であっても、その表現が非常に複雑になり、元の概念よりも理解しにくくなることがあります。
   • 圏論的な記述が常に最も自然で直感的な表現であるとは限りません。
3. 有用性の問題:
   • 圏論で表現できたとしても、それが常に元の分野に新しい洞察をもたらすとは限りません。
   • 圏論的な定式化が、必ずしも元の問題を解くための最も効果的な方法であるとは限りません。

まとめ

圏論は数学の多くの分野を統一的に記述できる強力な言語ですが、万能ではありません。具体的な問題を解決するためには、それぞれの分野に特化した手法や知識が必要となる場合も多いです。圏論は、異なる分野間の関係性を理解したり、新たな視点を得たりするための強力な道具ですが、それ自体が全ての問題を解決する魔法の杖ではありません。

圏論が最も力を発揮するのは、異なる数学の分野を横断的に見て、それらの間に隠れた共通の構造を発見し、それを利用して新しい定理を証明したり、概念を拡張したりする場合です。

はい、圏論が有効に働いた具体例として、ホモトピー型理論 (Homotopy Type Theory, HoTT) を紹介します。これは、圏論（特に高次圏論）と型理論（プログラミング言語の理論的基礎）が融合して生まれた分野で、数学の基礎論に革新をもたらしつつあります。

1. 背景：数学の基礎の危機と型理論

20世紀初頭、集合論に基づく数学の基礎に矛盾（ラッセルのパラドックスなど）が見つかり、数学の基礎を再構築する必要が生じました。一方、計算機科学の発展に伴い、プログラミング言語の型システムを扱う型理論が発展しました。

2. ホモトピー論の登場

ホモトピー論は、位相幾何学の一分野で、連続変形（ホモトピー）によって移り変わる図形の性質を研究します。例えば、コーヒーカップとドーナツは、連続的に変形できるため、ホモトピー論的には同じものとみなされます。

3. 圏論による接続：高次圏

ホモトピー論における「連続変形」の概念は、圏論における「射」の概念と対応付けられます。さらに、連続変形の間の変形（高次のホモトピー）は、高次圏（2-圏、3-圏、…）の概念と対応付けられます。高次圏は、対象、射、射の間の射（2-射）、2-射の間の射（3-射）… といった、高次の関係性を扱う圏論の拡張です。

4. 型理論との融合：ホモトピー型理論

型理論における「型」は、集合論における「集合」に対応し、「型の要素」は集合の要素に対応します。驚くべきことに、型理論における「型」の間の「等しさ」の概念が、ホモトピー論における「パス」（連続変形）の概念と深く関係していることが発見されました。

具体的には、型理論における「等しさの型 (Identity Type)」が、高次圏におけるパスの空間（path space）に対応することが示されました。これにより、型理論の枠組みで、高次圏論、ひいてはホモトピー論を展開することが可能になったのです。

5. ホモトピー型理論の成果

• 数学の新しい基礎付け: ホモトピー型理論は、集合論に代わる数学の新しい基礎となりうる可能性を秘めています。
• 計算機による証明支援: ホモトピー型理論は、計算機による証明支援システム（Coq, Agdaなど）との親和性が高く、形式化された数学の構築に貢献しています。
• 数学と計算機科学の融合: ホモトピー型理論は、数学と計算機科学の間の深い関係性を明らかにし、両分野の発展を促進しています。

なぜ圏論が有効だったのか？

圏論（特に高次圏論）は、ホモトピー論と型理論という、一見すると全く異なる分野を結びつける「共通言語」を提供しました。圏論の抽象的な枠組みがなければ、これらの分野の間の深い関係性を見出すことは困難だったでしょう。圏論は、数学の異なる分野を結びつけ、新しい分野を創出する上で、極めて重要な役割を果たしたのです。

はい、その理解で正しい部分と、さらに深い部分があります。

同じ概念を異なる表現で:

• 型理論における「等しさの型 (Identity Type)」と、ホモトピー論における「パス」は、表面的には異なる分野の異なる概念に見えますが、圏論（特に高次圏論）の視点を通すと、本質的には同じ構造を表していることが明らかになりました。
• これは、異なる言語で書かれた同じ物語のようなものです。言語は違えど、物語の構造や登場人物の関係性は同じ、という状況に似ています。

異なる数式や定理で:

• 型理論とホモトピー論は、それぞれ独自の記法、公理、定理体系を持っています。
• ホモトピー型理論は、これらの異なる体系を、圏論の言葉を「翻訳機」として使うことで結びつけ、一方の分野の定理を他方の分野の言葉で表現したり、証明したりすることを可能にしました。

さらに深い部分：新しい視点と可能性

圏論による接続は、単に「同じ概念の言い換え」にとどまりません。

• 新しい視点の獲得: ホモトピー論の視点を取り入れることで、型理論に新しい解釈や概念（例えば、高階の等価性）が導入されました。
• 新しい定理の発見: 圏論的な視点から、これまで知られていなかった型理論やホモトピー論の新しい定理が発見される可能性があります。
• 分野間の相互作用: 一方の分野の問題を他方の分野の言葉で表現することで、解決の糸口が見つかることがあります。

例え:

物理学における「波動」と「粒子」の二重性を考えてみてください。古典物理学では、これらは全く異なる概念でしたが、量子力学では、これらが同じ現象の異なる側面であることが明らかになりました。圏論は、数学の異なる分野に対して、これに似た役割を果たすことがあります。つまり、一見異なる現象の背後に、共通の数学的構造を見出すことを可能にするのです。

ホモトピー型理論は、圏論が異なる分野を結びつけ、新しい数学を生み出す力を示す、非常に強力な例と言えるでしょう。